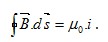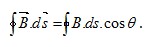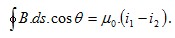CONSTRUÇÃO DO PROJETO COM TESTE (VÍDEO)

No vídeo abaixo é possível analisar os passos para a construção do Anel de Thomson e o teste demonstrando seu funcionamento.

Memorial de Cálculo

Antes de explicar sobre os cálculos realizados, gostaria de falar um pouco sobre as propriedades magnéticas dos anéis que foram utilizados no projeto. Mas por quê? Foram utilizados anéis de Ferro, Alumínio, Cobre e PVC. Cada um deles possui ou não propriedades magnéticas, com isso, podemos saber qual será o efeito causado no material quando o interruptor permitir a criação do campo magnético. Com isso, teremos:

Ferro → Propriedade: Ferromagnético (Será atraído fortemente pelo campo gerado).

Alumínio → Propriedade: Paramagnético (Possui elétrons desemparelhados e quando for submetido ao campo da bobina, seus elétrons ficarão alinhados no mesmo sentido do campo ao qual foi submetido).

Cobre → Propriedade: Diamagnético (Não será atraído pelo campo pois seus átomos criam um campo de sentido oposto).

PVC → Não possui propriedades magnéticas. Já que, é oriundo de orgânicos poliméricos sintéticos.

O primeiro passo que tivemos para os cálculos foi determinar a força peso de cada anel para que dessa forma, pudéssemos encontrar uma força magnética relativamente superior ao do material que possuir a maior. Sendo assim, através da massa específica de cada um, determinamos suas massas da seguinte forma:

          m_material = ρ_material.V

Sendo:

m → Massa (Kg)

V → Volume (m³)

ρ → Massa Específica (Kg/m³)

Dados:

h = 8 mm → 8.10^-3 m

r = 50 mm → 5.10^-2m                   *Volume dos anéis : (V = π.r².h) → V = 2π.10^-2 m³

Logo:

m_Cobre = 0,558 Kg

m_Alumínio = 0,169 Kg

m_Ferro = 0,496 Kg

m_PVC = 0,085 Kg

Após obter as massas, calcularemos a força peso para cada material através da segunda lei de Newton dada por:

          F = m.a

Sendo:

F → Força (N)

m → Massa (Kg)

a → Aceleração (m/s²)

Neste caso, a força será a força peso representada pela letra “P” e a aceleração será a da gravidade representada por “g”. Teremos:

*Considerando g = 9,81 m/s²

P_{Cobre =} m_Cobre . g = 5,474 N

P_{Alumínio =} m_Alumínio . g = 1,658 N

P_{Ferro =} m_Ferro . g = 4,866 N

P_{PVC =} m_PVC . g = 0,85 N

Com isto, temos todos os dados necessários relacionados ao conhecimento mecânico do projeto. Percebemos, que, o material com maior força é o cobre. Logo, necessitaremos que nossa bobina produza um valor que supere este. Coisa que, iremos determinar em seguida.

Mas antes disso, através das Leis de Ohm, determinaremos a resistência do fio e posteriormente a corrente elétrica que passará no mesmo. E para isso, foi utilizado uma tabela AWG que nos forneceu o diâmetro e a área da secção do fio nº 29, foi utilizado essa numeração devido ao custo-benefício pois era o que teria a corrente dentro da faixa desejada e economicamente viável. Permitindo então encontrar a resistência através da segunda Lei de Ohm dada por:

                  

          R = ρ.L/A

R → Resistência Elétrica (Ω)

L → Comprimento do fio (m)

A → Área da secção (m²)

ρ → Resistividade Elétrica (Ω.m)

Dados:

Diâmetro do fio = 0,2859.10^-3 m

Diâmetro de uma espira = 0,04 m
L = 2π.r → L = 0,04π. m (Porém, como serão 600 espiras, multiplicamos este valor por 600). → L = 75,3982 m

Área da secção = 6,47.10^-8 m

ρ = 1,72.10^-8 Ω.m

Sendo assim, teremos:

R = 20,044 Ω

Em seguida, utilizaremos a primeira Lei de Ohm para determinar a corrente elétrica que será dada por:

          R = V/I

Sendo:

R → Resistência Elétrica (Ω)

V → Tensão (V)

I → Corrente elétrica (A)

Dados:

R = 20,044 Ω

V = 220 V

Teremos:

I = 10,98 A

Desta forma, passaremos agora a tratar sobre o eletromagnetismo, partindo então, para o cálculo do campo de fluxo magnético e a força magnética para assim, comparar com as forças peso calculadas anteriormente.

É importante citar, que, foi escolhido o valor de 600 espiras para a montagem do projeto. Pois, quanto mais espiras, maior será o campo e consequentemente a força magnética. Evitando então, que a bobina não tenha a força desejada.

A fórmula para o campo magnético será dada por:

          B = n.I.µ/L

Sendo:

B → Campo do fluxo magnético (T)

n → Número de espiras

I → Corrente Elétrica (A)

L → Comprimento da solenoide (m)

µ → Permeabilidade magnética do vácuo (T.m/A)

Dados:

n = 600 espiras

I = 10,98 A

L = 75,3982 m

µ = 4π.10^-7 T.m/A

Logo:

B = 0,1098 mT

Em seguida, calcularemos a força magnética da seguinte forma:

          F_Mag = B.I.L.sen(ө)

Sendo:

F_Mag → Força Magnética (N)

B → Campo Magnético (T)

I → Corrente Elétrica (A)

L → Comprimento da solenoide (m)

ө → Ângulo entre o Campo e a Corrente

Dados:

B = 0,1098 mT

I = 10,98 A

L = 75,3982 m

ө =  90°

Logo:

F_{Mag =}   0,09 N 

E assim, concluímos os nossos cálculos para determinar a força magnética que será produzida pela bobina e com este valor poderemos falar sobre o efeito em cada um dos anéis citados no início do texto.

O anel de Cobre é o que possui o maior peso. Sendo assim, ele sofrerá a influência da força magnética porém a força oposta que é a peso será maior, então não ocorrerá a levitação magnética.

O anel de Ferro, também possui uma força peso maior. No entanto, a sua propriedade magnética que foi citada anteriormente, fará com que este seja atraído, ou seja, ele se moverá porém ele não levitará nem será movido para cima, sofrerá apenas o movimento de atração.

O anel de Alumínio, possui uma força peso bem menor do que a força magnética, e de acordo com a sua propriedade magnética, os seus elétrons se alinharão com o campo. Logo, pode-se concluir que ele sofrerá a levitação magnética.

O anel de PVC, como já citado anteriormente, não possui propriedades magnéticas. Sendo assim, ele não sofrerá nem atração nem repulsão, permanecerá em seu estado natural pois devido a composição de seu material ele não sofrerá influência magnética.

Agradecimentos

Olá leitor, 

"O talento vence jogos, mas só o trabalho em equipe ganha campeonatos"-Michael Jordan 

Essa frase resume tudo que aconteceu na realização deste projeto, pois além de cada membro da equipe se empenhar para fazermos algo bem feito e que funcionasse, alguns amigos nos ajudaram muito e o mínimo que podemos fazer é agradecer a grande ajuda deles são eles: Anderson Almeida Teles, Antonio Freitas Júnior, Giovanna Wen Ferreira,Ítalo Antonio de Santana Amorim, José Gilson Ferreira da Silva Júnior e Laís Moreira Silva. Além deles, gostaríamos também de agradecer a nosso Professor Targino Amorim Neto, que com esse projeto nos deu o objetivo de engenhar, de entender como um engenheiro em sua vida cotidiana pensaria parar resolver problemas que foram encontrados na execução do projeto, nos aproximando da realidade que nos aguarda ao término do curso e também agradecemos ao nosso orientador José Vicente Cardoso Santos que sempre, em todas as ocasiões sempre nos ajudou nos direcionando o que fazer.

Deixamos aqui o nosso muito obrigado!

Tabela AWG - American Wire Gauge

A tabela AWG é consultada constantemente por profissionais de rebobinamento de motores, fabricação de transformadores etc.

Essa tabela AWG é para fio de cobre esmaltado o, que vai de 000AWG até 52 AWG.  A tabela traz as seguintes informações, Seção em mm^2, Diâmetro em mm, Espiras por cm, Peso em gramas por metros, Comprimento em metros por kg, Resistência em ohms por metros, Freqüência Máxima com 100% do efeito skin em cobre e  capacidade em Ampere de ruptura a 20ºC. (ELETROAQUILA, 2015). 

      Fonte: Eletroaquila. 

Nós decidimos usar o AWG Nº29 devido ao custo- beneficio, pois foi o que com a corrente desejada, era mais economicamente viável.

Referências: 

ELETROAQUILA. Disponível em <http://www.eletroaquila.net/tabela-awg-mm>. Acesso em: 19 Ago 2017 

Lei de Ampère e o Anel de Thomson

Andre Marie Ampère (1775 – 1836) nasceu em Polemieux-Le-Mont-d'Or, próximo a Lyon, na França. Viveu no período da revolução francesa, que ocorreu em 1789. Não colocava ciência e religião em conflitos, segundo seu filho Jean-Jaques.

O grande feito de Ampère foi desenvolver a famosa lei circuital de Ampère. Estabelece que para descrever um circuito, em termos de campo magnético, corrente e permissividade elétrica em uma determinada região, pode ser aproveitada a simetria. Deste modo, poderia encerrá-la num circuito fechado com a requerida simetria, de modo a facilitar as análises.

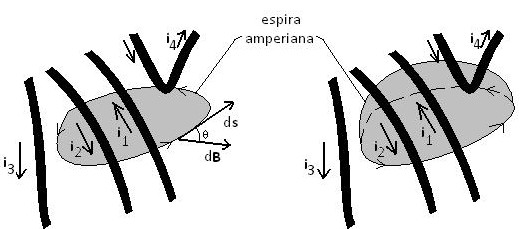
A integral no caminho fechado, percorrendo o circuito escolhido, resulta em uma equação que permite facilitar os cálculos para determinar o campo magnético produzido por uma região onde circula uma corrente elétrica, conforme mostra a figura 01.

Neste caso, são utilizados os elementos de campo magnético e os elementos de caminho percorrido pelo circuito escolhido. A lei de Ampère tem a seguinte forma:

A lei circuital de Ampère é conhecida como sendo mais fundamental que a lei de Biot-Savart, e conduz a resolução de problemas de forma mais elegante. Além do que é uma das quatro equações de Maxwell para o Eletromagnetismo.

Note que podemos escrever esta mesma integral utilizando o termo B.ds em função da direção de Be da direção dos elementos de caminho ds e do ângulo θ entre estes dois vetores. Desta forma, teremos:

As correntes i₃ e i₄ , apesar de contribuírem com o campo magnético no local, acabam por serem canceladas ao se fazer a soma de tais contribuições, uma vez que tem parcelas positivas e negativas, de mesma intensidade. No caso de i₃, a corrente entra e sai da região considerada. Já a corrente i₄ não atravessa a região envolvida pela espira amperiana. Deste modo, teremos, para a lei de Ampère, a contribuição resultante das correntes i₁ e i₂. No caso em questão, como uma das correntes entra e outra sai, teremos então como resultado:

Nota-se, portanto, que é necessário encontrar uma espira amperiana tal que B tenha valor constante ao longo da espira amperiana. Ou seja, B tem de estar numa região de alto grau de simetria.

Após a breve leitura sobre a Lei de Ampère, podemos dizer que a sua influência em nosso projeto está na análise do fluxo do campo magnético que será produzido pelas espiras ao longo do tubo. É importante ressaltar, que a lei será afetada pelo núcleo ferromagnético que estará na região interna do tubo para que o campo seja de certa forma amplificado e consequentemente, fazendo a força magnética ser maior e facilitando a levitação dos anéis.

Referências bibliográficas:
HALLIDAY, David,  Resnik Robert,  Krane, Denneth S.  Física 3, volume 2,  5 Ed. Rio de Janeiro:  LTC,  2004.  384 p. Disponível em:
<http://www.infoescola.com/fisica/lei-de-ampere/>
Acessado em: 07 Ago 2017

Lei de Faraday e sua aplicação no Anel de Thomson

Uma das descobertas mais importantes do que conhecemos hoje como eletromagnetismo foi feita pelo inglês Michael Faraday em 1831. Quando Faraday aproximou dois circuitos elétricos, percebeu que no momento em que um deles era ligado ou desligado, aparecia por um instante de tempo uma corrente no outro circuito. Percebeu também que o sentido da corrente era diferente se o circuito estava sendo ligado ou desligado. Para confirmar que era um efeito magnético, ele aproximou um ímã, e também observou o aparecimento de corrente. Essa corrente só se mantinha enquanto o ímã estava em movimento, e tinha sentido contrário dependendo se o ímã se aproximava ou se afastava. Ele também manteve o ímã fixo e movimentou o circuito, obtendo os mesmos resultados. A conclusão de Faraday é que a variação do fluxo magnético que atravessa o circuito produz uma tensão elétrica, que dá origem a corrente. Na verdade, a própria idéia de fluxo é devida em grande parte a Faraday, que imaginava linhas de campo emanando de cargas elétricas e de magnetos para visualizar os campos elétricos e magnéticos, respectivamente. Essa forma de pensar só seria aceita e usada de forma sistemática pelos cientistas após sua morte, mas sua importância pode ser percebida pelo fato de Maxwell ter dado a seu primeiro artigo, de 1856, o título “On Faraday’s lines of force”.

Assim, a Lei de Faraday enuncia que: "O valor da força eletromotriz induzida em uma espira de área A é igual à taxa de variação do fluxo magnético através dessa espira." Matematicamente, a Lei de Faraday pode ser escrita como:

ɛ = Força eletromotriz

-∆ɸ = Variação do fluxo magnético

∆t = Variação do tempo

ɸ = Fluxo magnético 

B = Campo magnético

A = Área da espira

θ = Ângulo entre o vetor campo magnético (B) e o vetor normal á espira (n)

A Lei de Faraday é uma das mais importantes que se relaciona com o Anel de Thonsom devido a mesma estar ligada à indução magnética, a qual vai permitir a levitação dos anéis.

Referência:

Lei da indução de Faraday. Instituto de Física de São Carlos. Dísponível em:<http://www.ifsc.usp.br/~strontium/Teaching/Material2010-2%20FFI0106%20LabFisicaIII/11-LeideInducaodeFaraday.pdf>. Acessado em: 09 Ago 2017.

Lei de Faraday- Neumann. Só Física. Disponível em: <http://www.sofisica.com.br/conteudos/Eletromagnetismo/InducaoMagnetica/leidefaradyneumann.php>. Acessado em: 09 Ago 2017.

LEI DE COULOMB

“A força de atração ou de repulsão entre duas cargas é diretamente proporcional ao produto do módulo das cargas elétricas e é inversamente proporcional ao quadrado da distância entre elas”.

O enunciado acima foi utilizado por Charles-Augustin de Coulomb para resumir sua tese. Halliday (2012) Duas partículas carregadas exercem forças uma sobre a outra. Se as cargas das partículas têm o mesmo sinal, as partículas se repelem, ou seja, são submetidas a forças que tendem a afastá-las. Se as cargas têm sinais opostos, as partículas se atraem, ou seja, são submetidas a força que tendem a aproximá-las.

Essa força de repulsão, ou atração é chamada de força eletrostática e a lei que permite calcular a força exercida por partículas carregadas é chamada lei de coulomb, que com base em experimentos em laboratório chegou a equação 1.0 que descreve matematicamente o enunciado da lei.

Equação 1.0

Para o desenvolvimento do projeto é importante termos conhecimentos da força elétrica, assim como da força magnética para entendermos a força eletromagnética, ou seja, uma partícula que está sujeita à ação de campos elétrico e magnéticos.

Referências

HALLIDAY, David; et al. Fundamentos de física: Eletromagnetismo. Ed. 9. Rio de Janeiro - RJ, 2012. 353 p.

Lei de Gauss e o anel de Thomson

Carl Friedrich Gauss foi um matemático alemão, o qual elaborou a lei de Gauss em 1835. Onde, a mesma relaciona o fluxo elétrico de um campo elétrico a partir de uma superfície fechada com uma carga (q) ao redor desta superfície.

Pela representação algébrica dizemos que a lei de Gauss é expressa por:

Com:

ε0 =   Constante de permissividade elétrica no vácuo.

Φ =  Fluxo elétrico resultante.

Q = Carga elétrica envolvida.

A partir desta fórmula e os conhecimentos obtido na teoria é possível identificar o sentido do fluxo a partir do sinal carga, onde se “q” for maior que zero, o sentido é para fora, se “q” for menor que zero, o sentido é para dentro. Tendo em vista que a carga “q” representa todas as cargas envolvidas ao campo sendo elas positivas ou negativas.

Por fim, com intuito de demonstrar um pouco na teoria este blog tem como principal objetivo representar e demonstrar o anel de Thomson que de certa forma possui grande parte devido a lei de Gauss, tendo em vista que o anel para levitar produz um campo magnético através da corrente elétrica induzida formando assim um fluxo que se identifica e pode ser ilustrado em parte pela Lei de Gauss.

Fontes:

· Fundamentos da Física, vol. 3 (Eletromagnetismo), Quarta Edição, Halliday, Resnick, Walker, Livros Técnicos e Científicos Editora S.A.

https://www.if.ufrgs.br/tex/fis142/mod03/m_s02.html.

http://mundoeducacao.bol.uol.com.br/fisica/lei-gauss.htm